Für die Bewertung von Informationen sind häufig Berechnungen notwendig. Es zeigt sich leider sehr häufig, dass Zahlenangaben oder Masseinheiten völlig falsch sind.
- Und das läßt sich herausfinden, wenn wir selber Berechnungen durchführen können.
- Quantitative Abschätzungen sind auf allen Gebieten eine große Hilfe, um schnell zu überprüfen, ob Zahlenangaben glaubhaft sind oder völlig falsch sein müssen.
Und deshalb werden wir hier verschiedene Berechnungsmethoden und Hilfsmittel diskutieren, wie:
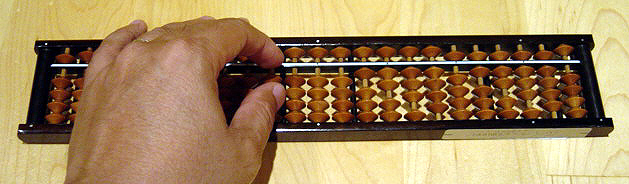
- Rechnen mit Rechenschieber und Abakus
- Rechnen mit Taschenrechnern
- Rechnen mit Kalkulationstabellen
Mit diesen Hilfsmitteln lassen sich schon sehr viele Berechnungen durchführen.
Als Ergänzung werden noch diskutiert:
- Geometrie- und Algebra- Softwareprogramme
- Programmieren in Fortran
Beipiel:
Wieviele Jahre werden benötigt, um die gesamte Staatsverschuldung des Bundes und der Länder zu tilgen ?
- wie hoch ist die Staatsverschuldung S des Bundes und der Länder insgesamt ?
- wie viel Geld G kann jedes Jahr investiert werden, um die Staatsverschuldung abzutragen ?
Nehmen wir zur Vereinfachung an, dass der Bund und die Länder keine Zinsen zahlen müssen, was heute sogar recht gut zutrifft, dann werden
N = S / G Jahre benötigt, um die Staatsverschuldung auf Null zurückzuführen.
Wenn wir in die Google Suchmaschine Deutsche Staatsverschuldung eingeben, finden wir, daß S = 2166 Milliarden Euro beträgt.
Nehmen wir an, dass die jährliche Schuldentilgung G = 10 Milliarden sein kann ( was seit Jahrzehnten nie erreicht wurde ) , so werden also
N = S / G = 216,6 Jahre benötigt.
- Bei einem Berufsleben von ca. 40 Jahren, werden also mindestens 5 Berufsleben benötigt.
Damit wir uns die Höhe dieser Staatsverschuldung anschaulich machen können, berechnen wir, wie hoch die Turmhöhe H aus 100 Euro – Scheinen ist, wenn jeder Euroschein 0,1 mm = 0,0001 m dick ist.
Dazu müssen wir folgendes berechnen:
Anzahl Z der 100 Euro-Scheine:
Z = 2166 000 000 000 /100 = 21 660 000 000
H = Z *0,0001= 2 166 000 m = 2 166 km
- Die Raumstation fliegt in 400 km Höhe
- Der Turm ist also mehr als 4 mal so hoch.
und er wiegt ( 100 Euro-Schein wiegt 1,02 g, also rund 1 g )
G = Z *1 = 21 660 Tonnen
( 1 Tonne = 1000 kg = 1 000 000 g )
Das Kreuzschiff Concordia zum Beispiel wog 115 000 Tonnen.
Diese Zahl ist beruhigend, denn dann können wir die Staatsverschuldung noch 5 mal mehr erhöhen, bevor unser Staatsschiff untergeht.
